この問題は、添付図の二つの長方形の面積が等しい事を証明する問題。
∠ＣＢＧ＝αと置くと、夫々の長方形の面積は：
S=a^2*(2*sinα)/(cosα+sinα)

∠ＰＡＢ＝θとすると：
S=a^2*(tanθ+1-1/cosθ)

これを図形的に証明してみて下さい（って、小生はまだ出来ていない）。

911.gc4 添付図のＡ、Ｂは定点（コマ大では樫の木と松の木）。
点ＣはＰをＢを中心に９０度時計回りに回転、点ＤはＰをＡを中心に９０度半時計回りに回転したもの。
点Ｃ、Ｄの中点をＱとした時、Ｑは常に一定である事を「ＣＡＤ的に」証明して下さい。

点Ｐを動かして遊んで貰っても結構ですよ。

前回か前々回あたりの「コマネチ大学数学科」という番組で
平面上に同じ大きさの正三角形が2つ別の位置に置かれているときに
片方をもう片方に重ねるような回転移動の中心の位置を作図しなさい
という問題が取り上げられてました。

面白い問題ですし，作図は直ぐに判ったのですが，
「それでよい」というのがどうも腑に落ちずに困っております。

つまり，「重ねることの出来る回転移動が存在する」
ということを前提にすれば，良いのですが・・・。

例えば，平面上に同じ長さの線分AB，CDがあり，
AをCに，BをDに重ねるような回転移動の中心Oを作図します。
「重ねることの出来る回転移動が存在する」ことが前提なら
それで終わりですが，
三角形OACとOBDが相似な二等辺三角形になるのは何故なのか？
が，小生の未熟な頭では上手く導けません。ご教授下さい。あ

図はNo.906を参照下さい。
∠ＰＡＢと∠ＣＢＧの比率は？
（数式で解く時に便利ですね！）

907.gc4 GCデータを追加しました。

Gogeometryを見ていて思いついた問題（元の問題は下記参照）

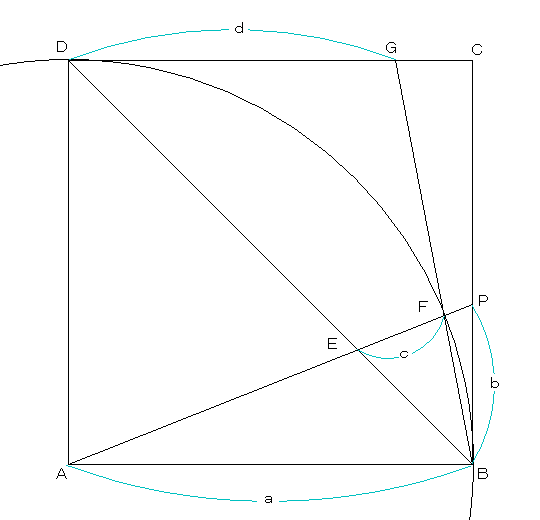
正方形ＡＢＣＤと図のようなＡを中心とする円、及びＢＣ上に１点Ｐがあります。
ＡとＰを結び、対角線と円弧との交点を夫々Ｅ、Ｆとし、ＢＦの延長とＣＤとの交点をＧとします。
２点間の長さを図のようにａ、ｂ、ｃ、ｄとすると：

ｄ／ｃ−ａ／ｂ＝１となる事を示して下さい（但し、点ＰとＢが重なる場合を除く）。

小生は数式では解けたのですが、何とか作図で証明出来ますか？
勿論、小生が出来た場合は、解答用ＢＢＳで発表しますが．．．（どうなることやら・・・）

gogeometry ⇒ problem/p394_square_arc_90_degrees_diagonal_congruence

Gogeometry（出題No.384）のコピーそのものです。
xがACに平行で、長さは三角形の外周の半分を証明せよ。

N/Tさんには易し過ぎる問題。

正方形と内接円、そして円上に点があります。
この点と、正方形の頂点、円との接点を図のように結び、４つの正方形を作ります。

この時、�@の面積と�Aの差は、�Bと�Cの差の２倍になります。

これはGogeometryからの引用です。
円の中心を原点とし、点Ｐの座標をｘ，ｙとすると簡単に解けてしまいますが、本音のＣＡＤ・ＣＡＭらしく、図形で証明して下さい。

解答No.947を見て、少し条件を付けました（この条件を外しても良いのですが、答えが複雑になりそう＝条件の仕分けが必要！）。

条件・・・円と直線は交わらないとする（Q893の図面を参考として下さい）。

これは酒転童子さんの解法にもある通り、２円の半径差を使って、１円に接し、中心が直線上にあり、かつ１点を通る円の作図になります。
それでも未だ出来ていないのですが．．．（２円の半径が等しい場合は無限に描けるし、一例を描くのも楽）

しかし、色々やっている内に「簡単な問題」が浮かびました。

１円、１直線、１点の条件で、求める円が描けない条件は何でしょうか？

ふっと気が付いて見直してみたら、メチャメチャ易しい問題でした。
そこで追記：
出来上がった正方形（の辺の長さ）と描いた円の半径の比率はどうなりますか？

２円Ｏ、Ｐがある時、図のように夫々の中心から接線を引き、接線と円との交点をＥ、Ｆ、Ｇ、Ｈとすると、四角形ＥＦＧＨは長方形になります。
単純に想像すると台形になりそうですが、これは eyeball theorem（眼球理論）と言うそうです。

この理論の証明では「本音のＣＡＤ・ＣＡＭ」らしくありませんね。

そこで、この理論を踏まえて（フシュウして？）：
１円Ｏと１点Ｐが与えられている時、四角形ＥＦＧＨが正方形になるような円Ｐを作図せよ。

昼休みの「やっつけ仕事」なので「穴」があるかも．．．

矢張りQ891の�Aの円を描いていて考えたのだが．．．
酒転童子さんの部屋に、１本の直線と２円に接する円の作図があるが
（http://www.k3.dion.ne.jp/~edo-cad/Apollonius'_problem_08.html）、
添付図のように１本の直線上に（円でも良いが）「中心」を持ち、２円に
接する円・・・描けるのだろうか・・・今の所小生には無理！

下の問題で、�Aの円を色々な方法で描いている内に見つけた問題。
添付図は円とその接線をベースに、円上に１点をとって描いた図形です。
図を見れば描き方は判ると思います。

ここで図の二つの長方形の面積が等しくなります。　証明して下さい。
まぁ、面積が等しいというか、ａ：ｂ＝ｃ：ｄの証明ですが．．．

図のように1/4円に半円が接しています。
�@は簡単、�Aも工夫すれば簡単、�Bは難しい？描ける？

昔々の問題の焼き直しです。
添付のように、球に１点マーキングしてあります。
定規とコンパスを使って（勿論コンパスだけでもＯＫ）反対側の点を求めて下さい。
今回は、コンパスでの長さコピー⇒表現が難しいですが、円を描いた後、コンパスの開きを固定して、別のところに「同半径」の円を描いて良いとします。

四辺形ＡＢＣＤとＡＥＦＧは正方形で、点Ｅは辺ＣＤ上にあります。
点ＩはＡＥとＢＣとの延長上の交点。
ここで長方形ＨＢＩＪを作ると、正方形ＡＥＦＧより小さくなります。

この差を作図で正方形に変形して下さい。

この時の正方形の１辺の長さを、Ａ〜Ｊの中から選んで示して下さい。

理由はどうでも良いです、とは言いませんが．．．

886.gc4 添付ｇｃを参照下さい。
�凾`ＢＣは直角二等辺三角形、水色の線はＡＢを直径とする円です。
赤線^2＝青線^2＋（青線−緑線）^2！
但し、点Ｄは円上の点で、辺ＡＢよりも上にあるとします。

Q882を一寸変えただけ・・・辺ＡＢの代わりに、∠Ａとしたらどうでしょう。
矢張り易しいか。

任意の三角形ＡＢＣの外接円と内接円を描きます。
この三角形の１辺（例えばＡＢ）の長さだけ残します（傾きを変えて）。

ここで三角形を消して、同じ三角形を復元するって、易し過ぎるか。

12×12の正方形を切って並べ替えたら・・・�Dは何処へ行った？

まぁ、実際にＣＡＤで描いて、夫々を並べ替えれば簡単ですね。

答えの割りに、問題図を作るのが面倒だった！

これは面白そう♪
時間が無いのについつい考えてしまう。

正方形ＡＢＣＤと対角線ＡＤが描かれています。
�@辺ＡＤ上に一点Ｐを取り、頂点Ｂと結ぶ
�Aこの線を点Ｂを中心に-45度回転する。
�B、�C上記の２線と対角線との交点を中心に図のように円を描く

この時、二重丸の３点は直角三角形の頂点である事を示しなさい。

さすがに、証明は無理な気がするッス。

酒転童子さんの「ＣＡＤで遊ぼう」⇒「１５年来の夢」から。
四角形に内接する楕円は無限に描けるのですが（コンパスと定規では無理）、その楕円の中心（焦点では無い）の軌跡が直線になるようです。

これってクイズになりますかねぇ。

ＧＣで遊んでいて見つけました。
３点Ａ、Ｂ、Ｐが在ります。
点ＣはＰをＡに対して９０度反時計回りに、点ＤはＢに対して９０度時計周りに回転したもの。

点Ｐを動かすと色々な線分ＣＤが出来ますが、ここで出来る線分には共通するものがあります。
それは何でしょうか。　出来たらその理由も答えて（証明して）下さい。

１点通過・２円接円
図の赤い円です。

�凾`ＢＣの中に点Ｐがあります。
この時�凾`ＰＢ＝�凾aＰＣ＝�凾bＰＡとなるように作図して下さい。

どうも、易しい問題か解けない問題しか浮かばないなぁ。

８５６が無くなってる気が？？？

ＣＡＤで描く場合、自由点又は交点等を結ぶ、既存線を伸ばす、交点を求めるが基本操作かな？

点Ｐが中点なら・・・作図してみて下さい。

「コンパスを使わない」だけでも、かなり難易度が違ってくるなぁ〜

解答用ＢＢＳには書きませんでしたが（書き忘れ？）、これってほぼ１００％正解に近づいているんです。

わざと、途中の易しい問題を飛ばして「作問」した効果があったかな♪

「同じ長さ」を定規で取って良いなら解けたけど…

出来ない（と思える）問題ばかりでしたので、易しい問題を！

平行四辺形ＡＢＣＤの（何処でも良いのですが）、１：２の内分点を求めよ。
勿論条件があります。コンパスは使えません＝定規だけでの作図です。

直径が等しければ簡単なんですが．．．

この場合、正方形の１辺の長さと直径の比率が１：５になりました♪
相似を使えば証明は簡単ですね。

上に行くほど、辺の長さ分が右にシフトするから長円（傾斜円？）に
なるのでしょうね。
これを上手く相殺する方法があれば・・・

添付図のように、正方形の１頂点の軌跡を見ると「長円」になるようです。
この傾きと扁平率が判り、作図可能であれば（定規とコンパスではなく、安価なＣＡＤで）答えは見つかるのですが．．．

尚、未だ「長円」となる検証はしていません。

添付図のように二つの円が接しています。
一点鎖線は共通接線です。

この線上に有り、頂点が円と接するような正方形の作図問題！

円の大きさ（比率）が出ていれば、力技で解けるのですが．．．

小生はまだ描き方が判っていません（出来ないかも）。

又、２円が接していない場合はどうでしょうか？
交わっている時は確実に正方形が存在しますが、離れた円の時は、存在しないケースも有りますね。

２次曲線でも、この直角三角形の内接円（中心）の軌跡は円弧なんですよね。
だから何なんだって！？！？
もう一本、単純な軌跡が出てこないか、未だ検討中です。

作図で解こうとすると、２次曲線になってつまずくんですよねぇ〜
計算での解なら、取りあえずはスッキリ。

これは「算法少女」と言う和算書からの問題で、ＣＡＤ的に解くのは大変かも．．．
小生は「算術的に」接円と大きな半円との半径比率で解を出して描きました。
結構簡単な比率になりました。

作図問題と称しながら、まったくの反則かも（反省です）。

尚、Ａ：Ｂ＝１：２や、Ａ：Ｂ＝２：１でも、かなり簡単な半径比率が得られました。
挑戦してみて下さい。

考え始めて３時間経過
脳が疲れた・・・(o_ △_)o
解けそうで解けないなぁ〜、これは難しい。

描き難そうな（悩みそうな）問題を作るのも結構大変だ。
これならどうでしょう。

半円Ｏと円弧上に一点Ｐが在ります。
図のように円弧と弦に内接する円、三角形に内接する円があり、前者は半径が最大となる円です。
例によって同じ半径となるような点Ｐを求めて下さい。

２点を通過し、１線と接する円（２点通過接円）

点Ｐを通過し、２線に接する円（１点通過２線接円）

830を解きながら、ふと思った疑問です。

問題　点Ｐから円Ｏへの接線

「結論」を知っていても作図は僕らにはパッと思いつきません。
これも有名な話なのかどうか？少なくとも私は初見。
面白そうなんですけどまだ良く考えていません。

糸口がつかめない…
というか、考えれば考えるほど新たな疑問が増えていく。
クイズのネタがいくつか出来たかも。

これってもしかすると、酒転童子さんの部屋に有りそうな作図だなぁ。
調べてみようっと！

与えられた「二等辺」�凾`ＢＣの辺ＢＣ上に点Ｐを取り、
�凾`ＢＰの内接円と�凾`ＰＣの傍接円（名称？？？・・・
図の通り）を描いた時、２円の径が等しくなるよう作図
して下さい ⇒ 点Ｐを作図で求めて下さい。