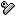 1342.txt
ڈ‰‚ك‚ؤ‚جڈo‘è‚إ‚·پB
1342.txt
ڈ‰‚ك‚ؤ‚جڈo‘è‚إ‚·پB
ƒRƒ“ƒpƒX‚ئ’è–ط‚ج‚ف‚جژg—p‚إپAچىگ}‚إ‚«‚é‚ئژv‚¢‚ـ‚·پBپi‚b‚`‚c‚جگ،–@پEٹp“x‚ج“ا‚فژو‚è‚إٹm”F‚µ‚ـ‚µ‚½‚ھپAڈط–¾‚ح‚ـ‚¾‚إ‚·پB“‚¢پEپEپEپj
‚b‚`‚c‚ھچD‚«‚بپAڈ¬پA’†ٹwگ¶‚ج•û‚à’§گي‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
چىگ}•û–@‚ھ‚ي‚©‚ء‚½‚çپA‚b‚`‚c‚ج–ت”’‚³‚ئ‹ء‚«‚ھ–،‚ي‚¦‚é‚ئژv‚¢‚ـ‚·پB
”¼‰~‚n‚ئ‚»‚ج’¼Œa‚`‚a‚ھ‚ ‚è‚ـ‚·پB
‚»‚±‚ة‚R‰~‚ج‚n‚PپA‚n‚QپA‚n‚R‚ھ“àگع‚µ‚ؤ‚¢‚ـ‚·پB
‚n‚P‚ح’¼Œa‚ئ‰~ژü‚ج‚`‘¤پA‚»‚ê‚ئ‰~‚n‚Q‚ةٹOگع‚µ‚ؤ‚¢‚ـ‚·پB
‚n‚R‚ح’¼Œa‚ئ‰~ژü‚ج‚a‘¤پA‚»‚ê‚ئ‰~‚n‚Q‚ةٹOگع‚µ‚ؤ‚¢‚ـ‚·پB
‚n‚Q‚ح’¼Œa‚ئ‰~‚n‚P‚ئ‚n‚R‚ةٹOگع‚µ‚ؤ‚¢‚ـ‚·پB
‚n‚PپA‚n‚QپA‚n‚R‚ح“¯‚¶”¼Œa‚إ‚·پB
“d‘ى‚ب‚µ‚إچىگ}‚إ‚«‚ـ‚·‚ج‚إپA’§گي‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢‚ثپB