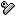 1352.xls
�R�[�q�[�^�C���ɂ��傤�Ǘǂ��Ǝv�����ł��B
1352.xls
�R�[�q�[�^�C���ɂ��傤�Ǘǂ��Ǝv�����ł��B
����́A��]���q����̕����𗘗p�����Ă��������A�����Ă��鎞�ɏo������}�ł��B�i��]���q���݂܂���B���������ɂ悭���ז����Ă��܂��B�j
���A���w���̕��ł��A�|���j�E�X�̉~�̖�肪��}�o����A�����ɉ���Ǝv���܂���B
����AB�ɐڂ��锼�a�̈قȂ�2�̉~ O1,O2 ������܂��B
�܂��A���� O1,O2 �̉~���m���O�ڂ��Ă��܂��B
�����ɒ���AB��ɒ��S�������~ O ����}���ĉ������B
�ȒP�߂�������?