 Gogeometry �Ɏ�����肪����܂����B�@�`�g���S���ƂȂ邻���ł��i�Y�t�}�Q�Ɓj�B
Gogeometry �Ɏ�����肪����܂����B�@�`�g���S���ƂȂ邻���ł��i�Y�t�}�Q�Ɓj�B
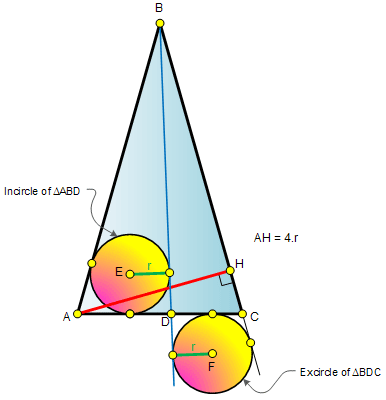
�}�����Ĕ���ʂ�Aincircle�����ډ~�Aexcircle���T�ډ~�ł��B
ex �ƌ����ƈꌩ�O�ډ~�݂����ł����A�O�ډ~�́Fcircumcircle�I
�����ł͉������̂ł����A�}�`�I�ɉ����ɂ́H�H�H�i��킪�\�z����܂��j
�b�`�c�ō�}���đ��肷��ƁA�덷�͈̔͂Ő�������������܂����D�D�D
�����ł̉������́i�������j�F
��p���u2�Ɓv�A�`�A�a�����_����}�P�Ƃ��A�`�̍��W���iAx,Ay�j�̂悤�ɕ\���ƁA
Ax = -1, Ay = 0
Cx = 1, Cy = 0
Bx = 0, By = tan(2��)
�~�̔��a�����Ƃ��āA
�E�E�E�i�����j
�S�Ă��ƃƂ݂̂ŕ\���o���A����ǂ��Ă����Ɠ������o�܂��B
�������A���s���Ȃǂ������A�ǂ�����Đ}�`�I�ɉ����̂��Ȃ��i�撣��˂j�B