 ‚±‚ج–â‘è‚à‚ي‚©‚èˆص‚¢‚و‚¤‚ةپAگ”‰ٌ‚ة•ھ‚¯‚ؤ
‚±‚ج–â‘è‚à‚ي‚©‚èˆص‚¢‚و‚¤‚ةپAگ”‰ٌ‚ة•ھ‚¯‚ؤ
“ٹچe‚·‚é—\’è‚إ‚µ‚½‚ھپAژٹش‚ج“sچ‡‚إپA–{–â‘èˆê‘è‚ئ‚µ‚ـ‚µ‚½پB
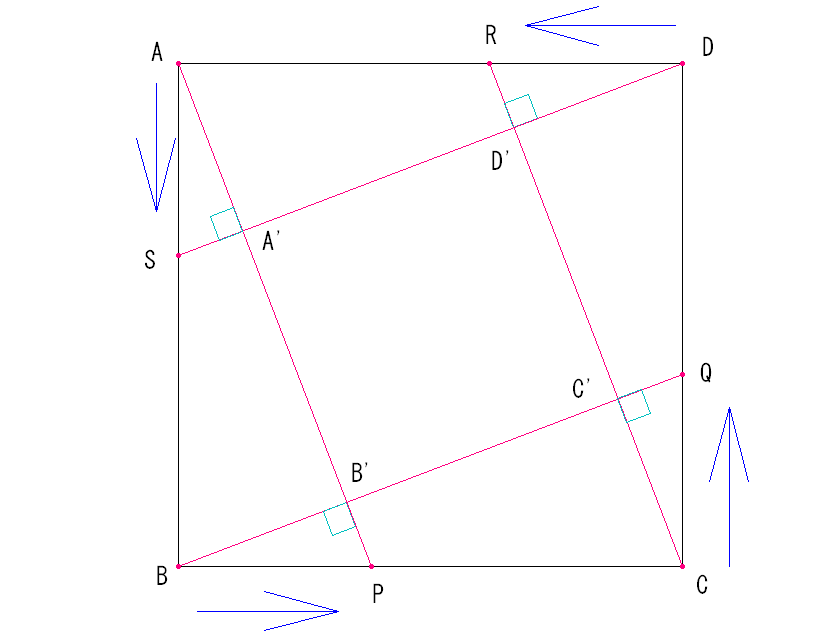
‡@پ@ˆê•س‚ھ2‚جگ³•ûŒ`ABCD‚ھ‚ ‚è‚ـ‚·پB
‡Aپ@A‚©‚ç“_SپAB‚©‚ç“_PپAC‚©‚ç“_QپAD‚©‚ç“_R‚ھ
پ@پ@“¯ژ‚ةگآ–îˆَ‚ج•ûŒü‚ة“¯‚¶ƒXƒsپ[ƒh‚إگi‚ف‚ـ‚·پB
‡Bپ@A‚ئ“_PپAB‚ئ“_QپAC‚ئ“_RپAD‚ئ“_S‚ً‚»‚ꂼ‚ꌋ‚ر‚ـ‚·پB
‡Cپ@ˆع“®‚ج“r’†‚إ’¼گüAP,BQ,CR,DS‚ھ‚آ‚‚éگ³•ûŒ`A'B'C'D'‚ج–تگد‚ھ
پ@پ@گ³•ûŒ`ABCD‚ج1/3‚ة‚ب‚éژ‚ًƒRƒ“ƒpƒX‚ئ’è–ط‚إچىگ}‚µ‚ؤ‚‚¾‚³‚¢پB