 ������Ăǂ��`����ł��������H
������Ăǂ��`����ł��������H
�~O��O��ʂ钼��������A�~A�i�ԁj�͉~O�Ƃ��̒����ɐڂ��Ă��܂��B
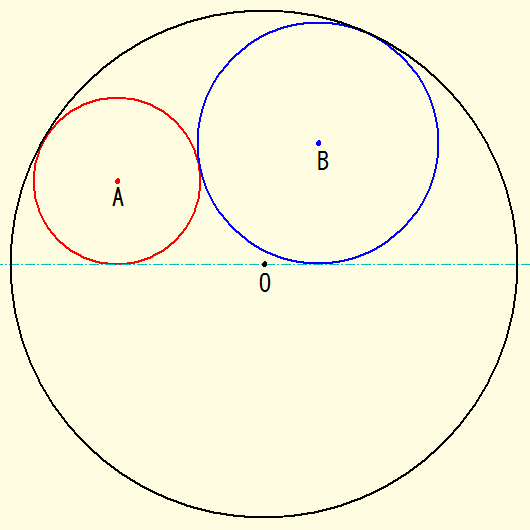
���̎��A���~�ɓ��ڂ��ԉ~�ƊO�ڂ��A�����̒����ɐڂ���~B�̍�}�ł��B
����������ŋA��A���Ď����ŏo�肵�������������Ƃ��ăp�^�b�Ǝ肪�~�܂�܂����B
��]���q����ɂ��A�Y������~B�͂R�`���锤�ł��B
�~B�́u�ȕւȁv��}�@�́H�H�H
JWWCAD�R�}���h���g���ΊȒP�Ȃ̂ł����A�O��������K�ƃR���p�X�ŁI
�ǂ������݉߂��̂悤�ŁA�����A�{�i�I�Ɏ��g�݂܂����D�D�D
���݉߂��E�E�E�뎚�E�����炯�����m��܂��A���e�͂��B