酒転童子さんへ：

これは貴兄（禁句！）の作品の完全なパクリですので、解答の方のフォローをお願いします。
ズゥズゥＣ？

ヒントになるかどうか判りませんが．．．（ＧＣによるヒント？）
http://fukuchande.gozaru.jp/malfatti_general.html


二等辺三角形なら、ＧＣでも楽に描けますが、この描き方は参考になりません！
http://fukuchande.gozaru.jp/malfatti_exception.html
（見ると混乱するだけかも・・・）

解けそうで解けない・・・

出題図はこちら ⇒ http://www.k3.dion.ne.jp/~edo-cad/malfatti.html

酒転童子さんにとっては常識的作図なので、敢えて出題されていないようですが、結構面白い作図法です。
ただし、出来上がった図から「完成」を確認していますが、小生には理屈が上手く説明（証明）出来ていません。

末筆ながら、酒転童子さん！無断拝借ご容赦ください。

なかなか面白そうです♪

最近はN/Tさん以外、反応が無いので、早速ヒントです。

解答用ＢＢＳからリンクが貼られていますが、「ようこそ酒転童子の部屋へ」を参考にして下さい。

http://www.k3.dion.ne.jp/~edo-cad/kakezan.html

酒転童子さんが最初に答えるのかな？

正七角形では、１頂点から他の頂点へ６本の線が引けます。
外接円の中心（外心）をＯとした時、ＡＢ×ＡＣ×ＡＤ×ＡＥ×ＡＦ×ＡＧ÷ＯＡ^6＝７を、ＣＡＤで説明して下さい。

正ｎ角形の外接円の半径をｒとし、頂点同士を結んだ線の長さをａ１、ａ２・・・、ａｎ−１とした時、ａ１×ａ２×・・・×ａｎ−１÷ｒ＾（ｎ−１）＝ｎとなる七角形ヴァージョンです。

長さＬの線分を正２角形と表現すると、ｒ＝Ｌ/２ですので、Ｌ/ｒ＝２！
正三角形、正方形、正六角形等は数学的な証明は楽ですが、正ｎ角形の場合の数学的な証明に挑戦する人は？？？

正七（多）角形について、酒転童子さんが大分疑問を抱いているようなので（彼のサイトをご覧下さい）、少し安心して頂けるようにと考えました。

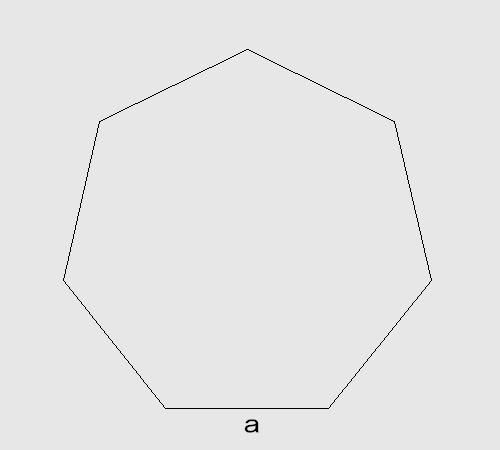
ＣＡＤコマンド（回転や多角形）を使って、添付図のように１辺ａの正七角形を描いて下さい。
対角線は全部で１４本引けますが、長さは２種類だけです。
これをｂ、ｃとした時、１／ｂ＋１／ｃ＝１／ａ が成り立ちます。
この事をＣＡＤで証明（説明？）して下さい。

逆に言うと、ＣＡＤコマンドで描いた正七角形で、上記をＣＡＤで表すことが出来れば、そのＣＡＤとしては正七角形が描けていると判断して良いと思います。

尚、小生が普段遊びで使っている２Ｄ−ＣＡＤでは、ソフトの精度範囲で数値が合いませんでした（正多角形コマンドは無いし、360/7 と言った計算式入力が出来ないので．．．他のソフトで作成し、ＤＸＦで読み込んだ場合はＯＫ！）。
勿論、Alibre Design Xpress ではＯＫでしたし、ＪＷ−ＣＡＤでも精度範囲内で等式が成り立つ事が証明できました。

アドレスというか、一部のアルファベットが入っていると投稿できない状態に
なっていました。m(_ _)m
現在は修正しています。

かなり難しい・・・

前に酒転童子さんの解法を使って、ＣＡＤの拘束機能で２の三乗根を求めました。
では、拘束機能を使わないで、三乗根を求められますか？

絶対出来ないとの答えでも構いませんが．．．

３Ｄ−ＣＡＤを使っていれば、理屈としては解ける筈です。

＞でも、「解けない」が答の問題も面白いかも♪

前に出題された「酒転童子さん」の問題の焼き直しですので、同じ解法で解けると思います。
添付図左は「正六角形に内接する六角形から、元の正六角形を再現せよ」で、右は括弧内の「六」を「五」に置き換えただけです。

五角形の方が、少し工夫が必要かも知れません。

削除しておきました。
でも、「解けない」が答の問題も面白いかも♪

小生は昨日、変な問題を出していますねぇ！
まだ酔っぱらう時刻ではないのに？？？

N/Tさん、削除しておいて下さい。
これは２つの形状があって、手の中ですり替えることによって、相手の目を白黒させるオモチャなんです。

もしも解こうとして考えていた人が居たらごめんなさい m(_._)m

＞昨日リンクさせて頂きました。

今朝（早朝）だったかも．．．

酒転童子さん、今晩は

言い忘れていました。昨日リンクさせて頂きました。
標題のＧＩＦファイルをパクリました、ご容赦を・・・

　みなさん、こんばんは。

　FUKUCHANさん、さっそくリンクして頂き、ありがとうございます。
　これからも、よろしくお願い致します。

酒転童子さん、お早う御座います。

あんなもので良ければ．．．かえって光栄です。
今、手抜き部分を中心に、見易く＆判り易く出来るよう、更新を検討中です。

　N/Tさん、FUKUCHANさん、こんばんは。

　N/Tさん、ごめんなさい。この場を貸して下さい。

　FUKUCHANさんのページ、リンクさせて下さい。
　よろしくお願い致します。

バナー使わせていただきました。

リンクありがとうございます。
　リンクはテキストリンクで充分ですが、もしバナーを使うならリンク集に
置いてあります。

ここで発言して良いか判りませんが、小生の回答集にこちらへのリンクを貼りました。
問題に行き詰まって、「ＣＡＤ」「図形クイズ」で Yahoo 検索したら、小生のページが最初に出てしまったので、慌ててＨＰ修正しました（ここの解答用ＢＢＳを見た人しか訪問して来ないと「高を括っていた！」）。

バナーは使った方が良い？？？

用済み後は、適切にこの発言を削除して下さい。

2Chan からヒントを得た息抜き問題です。

添付図は、或人の終戦記念日の行動に対する世論調査結果です（勿論、マスゴミ）。
調査結果（パーセンテージ）もグラフも、一切ダマシは無いと言ってます。
どうなっているのでしょうか？

接球描画の試行錯誤の結果、基本として又接円に戻って検討しています。
前に３点に接する円を描けとか言って、出題・解答を掲示しましたが、酒転童子さんの部屋に掲載されていたのですね！（一言仰って頂ければ⇒お恥ずかしい。少なくとも、ここに登場する人達の部屋は覗いてみないといけませんね）。

さて、試行錯誤の中で、簡単な問題なのですが（酒転童子さんの部屋を参照すれば）、上記に記載されていない問題形式を考えました。

添付図、１点、１円、１線が与えられているとき、１点を通り１円に接し、且つこの直線上に中心を持つ円を描いて下さい。
酒転童子さんの解法で解けます・・・チョットした頓智問題！
それにしても、これもアポロニウスの円だとは・・・出題していながら知らなかった（汗、汗．．．）。

数式で表してしまうと、味も素っ気もないですが、このようなファンタスティックな問題を作るのも面白そう！

こういうのも面白いかも？
http://pya.cc/pyaimg/pimg.php?imgid=1134

３点×１球で（２点×２球、１点×３球は、まだ手掛かり無し）、接球が描けない例がありました・・・これだけ？
３点を通る円が、１球と交わってしまう場合は、３点と球面で接する全ての球が、この１球と交わってしまいますねえ。

これは単に、四面体の内心を求めよと言う問題とほぼ同じですね！

２点×２球、１点×３球・・・作図の糸口も見つからない！
勿論、作図不可能と言う結論にも達していない！！！

３点１球の作図から、四面体を包含する（四面体の頂点が、球の表面にある）接球が描けることが判ります。
それでは、四面体に内接する「球」を描いて下さい。

３点を通る球の中心の軌跡は直線なので、２Ｄ−ＣＡＤでもう一つの球との接球を求めることが出来る。
２点と２球、１点と３球の場合、どうしても双曲面が出てきてしまうが、２Ｄで２点１円の接円を求めたように、２点２球を３点１球に収束出来ないのか！

皆さんの解法・ヒントを待っていますが、その整理として、３点１球の場合の接球の求め方を纏めて報告します。

説明がチョット厄介なので（と言う程でもない？）、解法を整理してからアップしますので、是非お知恵を拝借したく。

頭が硬くなっているのを実感します・・・（Ｔ∇Ｔ）

解法を見ると「な〜〜んだ！」となりますが（なると思いますが）、数学的に証明しようとすると、補助線の引き方でチョット苦労するかも知れません。

本当は「描け」＆「何故求められるか証明せよ」とする積もりでした。挑戦して下さい。

長方形⇒平行四辺形でも出来ますね！

与えられた長方形の辺の中点を、定規だけで（コンパスを使わずに）求めて下さい。

No.348 はグレードダウン（？）の新しい問題です。
すなわち、空間に３点と１球が与えられた時、球の表面がこの３点を通り、且つ１球に接するような球を描け！

取り敢えず３球の径が同じ場合には、割と簡単に描けました。
添付図は４球が接していませんが、お互いに接していても同じ描き方が出来ます。

まず３Ｄ−ＣＡＤ（Alibre Design Xpress）で４球を描き、これを２Ｄに落としました（２Ｄ画像が見易いように、３Ｄ作画では向きを工夫）。
２Ｄにて接球（名称？？？）を描き（径を求め）、それを３Ｄに読み込んで球を作成。
後はアセンブリで外接拘束を掛けたものです。
これは３点が球の表面にあり、別の球に接する球の描き方（表現が難しい）。

３点・１球が出来たので、次は２点・２球、そして１点・３球が出来れば、４円に接する球が描けるのですが．．．（道はまだ遠い？）

＞添付図は１例です。

１例と言いましたが、鏡面対称か、後はその回転形しかないですよね！

与えられた４本の線分を半径（直径）とし、お互いに接する球を描いて下さい。
添付図は１例です。
縮尺を１／２で描いたと見るか、線分を直径とした球と見るか・・・同じですが．．．

No.344/345 の解を見つけるための準備ですが、これをやっても見通しが立たない！
２次元だと三角形の頂点を中心とし、お互いに接する３円を描けますが、３次元の場合、四面体の頂点を中心とする球は、必ずしも４球が接するとは限らない！
難しいのか、何かコツがあるのか．．．

お互いに外接している方が、設計的かな？？？
Alibre で描きましたが、これは４球が同半径・・・小さい球の半径は計算式（sqrt なども使用）で入力。
外接拘束を掛けました⇒お互い全て拘束可能⇒数値が誤差範囲で合っていると言う事になりました。勿論干渉ゼロです。
これでもまだ、一般的な描き方が浮かびません．．．

今度は接円ではなくて、接する球（「接球」と呼ぶのか？）に凝り始めた。

・四つの球がお互いに接しています。この４球の接球（？）を描いて下さい。すなわち、この球の半径を求めて下さい。
・出題者はまだ出来ていません⇒本当のことを言うと「教えて下さい」なのです（中学までの数学で解ける筈・・・かな？）。

４球の半径（直径）が等しい場合は、正４面体を使って簡単に（？）この球の半径（直径）が判りますが・・・（添付図参照）

与えられた球の大円を描いて下さい（直径を求めて下さい）。
但し、添付図のような治具は使えません。コンパスと定規だけです（紙と鉛筆は常識！）。
勿論、球の表面に作図可能とします。
これも義務教育の数学の範囲で解けますね！

飽きもせず接円で遊んでいますが、添付図の２線と１点の作図に於いて、２線の交点が作図限界（？）の範囲で求められない場合、言い換えると、２線の交点を使わずに、１点を通り２線に接する円を描いて下さい。

勿論、ＣＡＤの接円コマンドは禁じ手です。

（理屈は簡単ですが、手続き＝描画手順が面倒臭いだけ？）

添付図では（見づらいかも知れませんが）８個の接円（黒円３個に接する円）が描けますが、一つも描けない事があります。
この一般解を判りやすく答えて下さい。

小生が家で使っている HO_CAD では、簡単に接円が描けないので、どうしてもこういう問題になってしまう．．．（JW_CAD なら楽に描けますが）

これは作図問題ではありませんので、ＣＡＤコマンド（拘束含み）をフルに使っても構いません。

>　基本が理解できていないのに、解き方だけはそれなりに一流！

私は詰め込み世代ですが、基本はしっかり叩き込まれました。
落ちこぼれを無くすはずのゆとり教育は、結果的に「基本よりも成果」
になっちゃいましたね。

＞理系知識を教る能力を持った先生が居なくなったのでしょうねぇ・・・

理系を理数系と置き換えて良いと思いますが、小中学校の理数系の先生は、凄い実力の持ち主ですよ。
基本が理解できていないのに、解き方だけはそれなりに一流！（最近は、高校受験問題が解けない中学教師などが話題ですが、これは格別）

教育の衰退は全体的に酷いですが、特に理科の凋落ぶりは凄まじいと思います。
理系知識を教る能力を持った先生が居なくなったのでしょうねぇ・・・

＞頭が固くなってるのだろうなぁ・・(　┯_┯)

いぇいぇ、ＣＡＤの進歩が素晴らしいのでしょうね！
複写（移動）コマンド一つとっても、定規とコンパスなら平行四辺形を描いて・・・

ただ、前にも発言しましたが、Black Box 化してます。　これは、技倆の進歩には繋がりますが、技術の進歩とは別ですね。
最近の子供達は、問題の「解き方（テクニック）」だけ憶えて、それなりに好成績を残すので（又、そのような教育をしているようなので）、使わなければいけないと言う義務だけ負わされる地位にいると苦労します。

小学校や中学の理数系の授業参観すると、完全に将来に失望します（全部見た訳ではありませんが、理解させる教育ではなく、点を取る教え方と！・・・昔は私立や塾だけでしたが、今は公立でも．．．）

すぐに解けるのだけど・・・
頭が固くなってるのだろうなぁ・・(　┯_┯)

基本的なことを、一つ一つクリアにしていくのが大事だと思いますので、冷静になる為に基本的な作図を！
添付図で２円と１直線が与えられています。
この直線を半径とする内接円（＆外接円・・・これは線分の長さや円の位置によっては作図不可能）を描いて下さい・・・基本に帰って冷静になる為の問題です。

頑張ったけど私も円−円接円が描けなかった・・・
これが若い世代になると、正確に描ける人は殆ど居ないでしょうねぇ〜