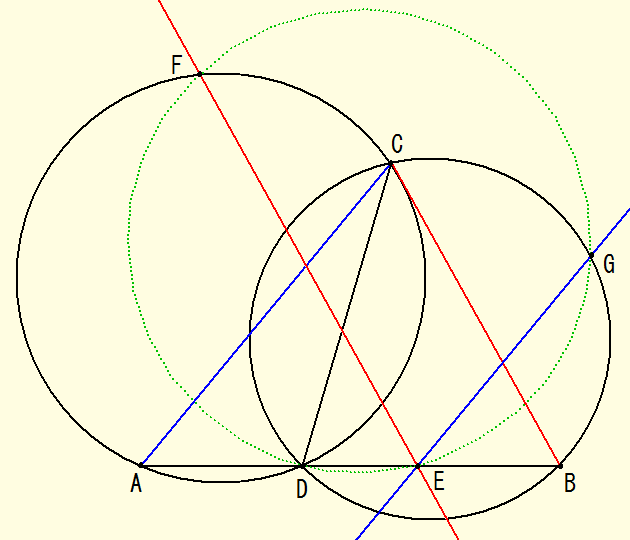
 ⊿ABCと辺AB上に点Dがあります。
⊿ABCと辺AB上に点Dがあります。
⊿ADCの外接円をO1、⊿DBCの外接円をO2とします。
次に辺AB上に点Eをとり、EF//BC、EF//ACとなる点FとGを求めます。
但しFは円O1上、Gは円O2上にあります。
この時、D、E、G、Fは同一円上にある事を証明して下さい。
これはかなり前にGeoGebra遊びのページに記載していましたが、3D遊びに夢中でほったらかしていたものです。
小生は座標では直ぐに解けたのですが、図形的にはまだ解けていません。
F、C、Gが同一直線上にある事、AF//BGである事を使うのか?
尚、同一直線や平行の証明にも挑戦してみて下さい(こちらは簡単だと思います)。
しかし、2D-CADコマンド(ショートカットキー)で少し躓いてしまった!!!(歳とると忘れるのも早い)