 下記の解答No.5229を参照して下さい。描き方はこれで判ると思います。
下記の解答No.5229を参照して下さい。描き方はこれで判ると思います。
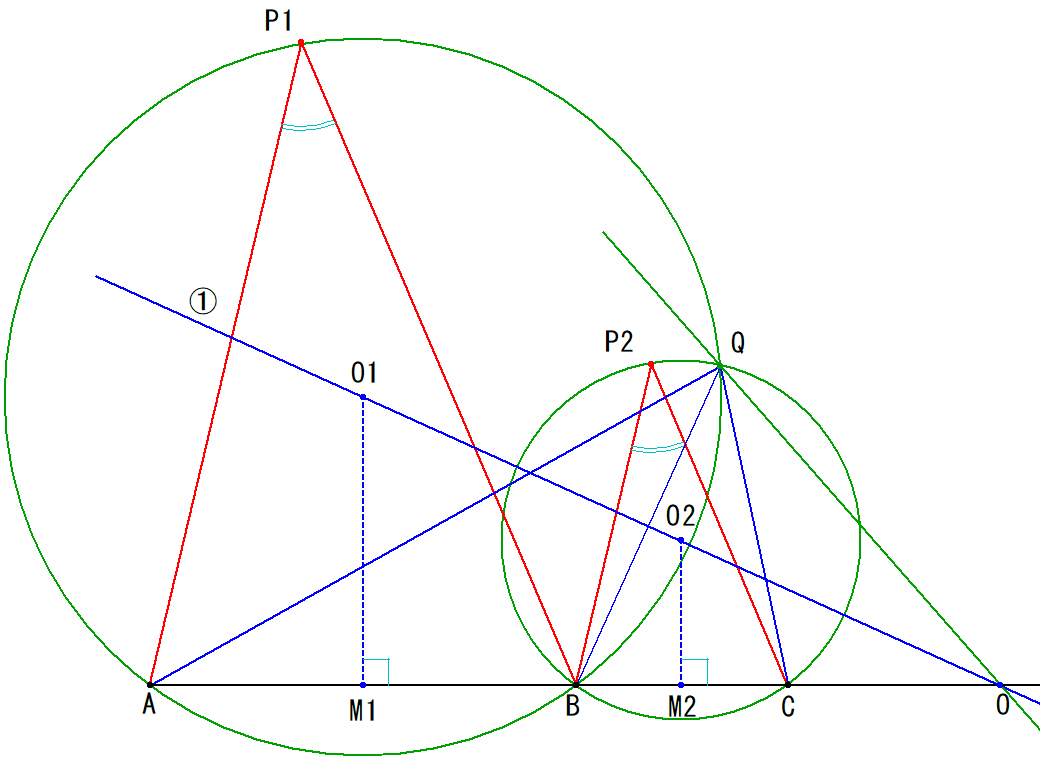
ここで、⊿P1ABと⊿P2BCは相似であり、相似比はAB:BC=2:1。
従って、円O1と円O2も2:1になり、①のように青線を引くと、点Oが求められます。
⊿P1AB:⊿P2BC=2:1である限り、その大きさに関わらず点Oの位置は変わりません。
又、O1、O2から黒先ABに垂線を下ろし、黒先との交点をそれぞれM1、M2とします。
M1、M2は赤三角形の底辺の中点ですから、線分M1M2=M2O=3BC/2、即ち、CO=BC。
OQは①の青円に対して、OAと対称な線になります(言い換えるとBとQが対象)。
即ち、OQ=OB=一定・・・点Oが不変でOQが一定ですから、点Qの軌跡は円になりますね。
説明が(添付図も)たどたどしくなってしまいましたが、これで説明は終わりです。但し、この円が黒先と交わる2点は除外(極限を含むとすれば完全な円)。