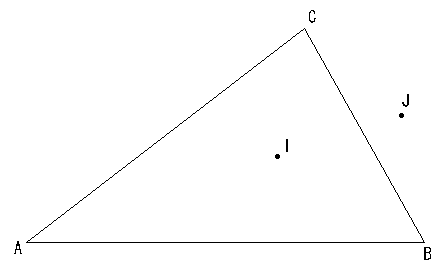
 ⊿ABCがあり、その内心をIとします。
⊿ABCがあり、その内心をIとします。
⊿BCIの外心をJとした時、3点A、I、Jは同一直線上にある事を証明せよ。
※これはIMOの問題を一部抜粋&変形したものです。易しくなり過ぎ?
元の出題文は↓・・・こちらを解いても良いですよ。
Let ABC be a triangle with incentre I. A point P in the interior of the
triangle satisfies
∠PBA + ∠PCA = ∠PBC + ∠PCB.
Show that AP ≧ AI, and that equality holds if and only if P = I.