 �܂�f(x)���`���܂��i�R�}���h���C����f(x)=3x^2+4x+5�Ɠ��͂��邾���j�B
�܂�f(x)���`���܂��i�R�}���h���C����f(x)=3x^2+4x+5�Ɠ��͂��邾���j�B
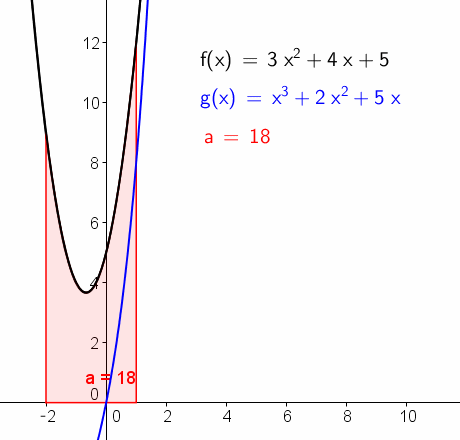
����y=f(x)�Ƃ���Ɛ}�̕�������`�悵�Ă���܂��B
integral[f(x)]�ŕs��ϕ��̎��ƋȐ���\�����܂��i�ϕ��萔��0�j�B
integral[3x^2+4x+5]�ł������ł����A�F�X�ȍ�Ƃ��l����f(x)���`�����̂ł����B
�Ԃ̖ʐς́Aintegral[f(x),-2,1]�ƒ�ϕ��Ōv�Z�������̂ł��B
���Ȃ�g������Ă���̂�Mathcad���͊y�ł����A���̕\���@�\��Mathcad����̂悤�ł��ˁB