 ��CAD(JW-WIN)�̏ꍇ�A���̒��x�̌덷�Ȃ�E�E�E
��CAD(JW-WIN)�̏ꍇ�A���̒��x�̌덷�Ȃ�E�E�E
�����S�z�ɂȂ�܂����̂ŁA���Ԃ��L�邤����UP���܂��B
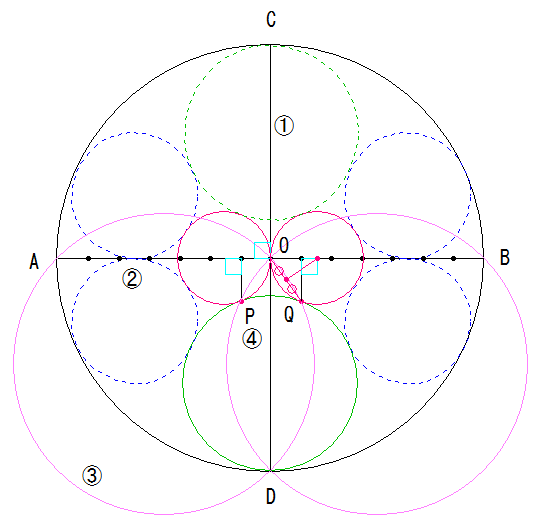
�@�@�~O�ɐ����Ȓ��aAB,CD�������܂��B
�A�@���aAO,OB�����ꂼ��7�������A
�@�@O����1:6�̕����_��萂�������낵�܂��B
�B�@3�_AOD�ABOD��ʂ铍�~�����ꂼ��`���A
�@�@�A�̓��~�Ƃ̏㕔��_��P�AQ�Ƃ��܂��B
���_D,P,Q��ʂ�~�����߂�Ή~�ł��B
�@�i�ԉ~��P(Q),O,���aAB��p����Ε`���܂��B�j
�c��̐~���A�|���j�E�X�̉~�̍�}�@���ŕ`���܂��B