 �Q�_A�AB�ƁA����AB�ɕ��s�Ȑ����^�����Ă��鎞�ANo.4724��N/T�������̒ʂ蒆�_�����߂��܂��B
�Q�_A�AB�ƁA����AB�ɕ��s�Ȑ����^�����Ă��鎞�ANo.4724��N/T�������̒ʂ蒆�_�����߂��܂��B
����AB���ԉ~�ƂQ�_�Ō����A���ԉ~�̒��S��ʂ�Ȃ����ANo.4727�̂悤�ɕ��s�������������o���܂��B
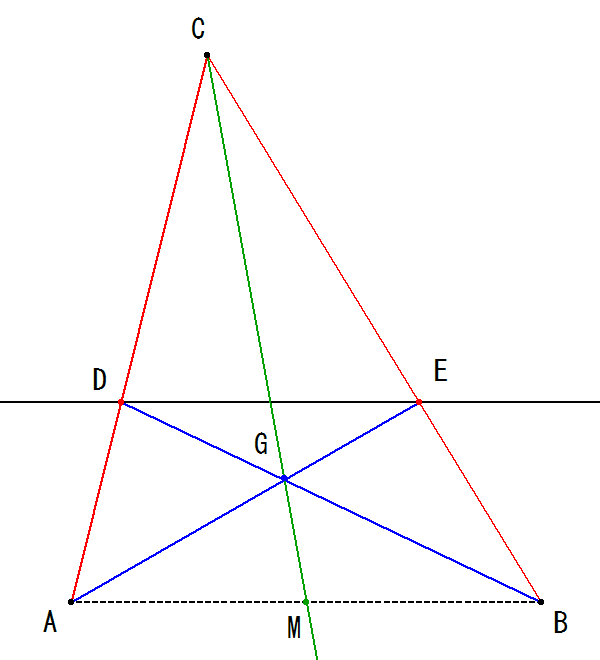
�K���ȏ��ɓ_C�����i�}�Q�Ɓj�AAC�ABC�Ƃ��̕��s���iNo.4727�̕��@�ō�}�j�Ƃ̌�_��D�AE�Ƃ��܂��B
����AE��CD�Ƃ̌�_��G�Ƃ������A����CG��AB�Ƃ̌�_���A���_M�ɂȂ�܂��B
�]���āAQ1883�@�ŏ�q�̂悤�Ȑ���������A���̒��_���K�݂̂ŕ`�������o���܂��B
�ł́AAB���~�ƌ����Ȃ�����~�̒��S��ʂ��Ă��܂����E�E�E���ꂪ�Y�݂Ȃ�ł��˂��B
moonlight����K�ȉ��o��̂ł́H�Ɗ��҂��Ă��鍡�����̍��ł��B
���A�ʐςł̐����𖾓��ȍ~�Ɍf�ڂƌ����܂������A�Y�t�}�̇�ADB����AEB�i�ʐρj���瓱���o����ł��傤�I�i�i�X�ʓ|�L���Ȃ����̂ŁA����Ő������I����Ă��܂������E�E�E�j�B