 No.4318���g���ė^�����Ĕ䗦�̐ԉ~�E�~��`���Ίy�Ȃ̂ł����E�E�E
No.4318���g���ė^�����Ĕ䗦�̐ԉ~�E�~��`���Ίy�Ȃ̂ł����E�E�E
�g��E�k���E��]���g��Ȃ����@�ł��B
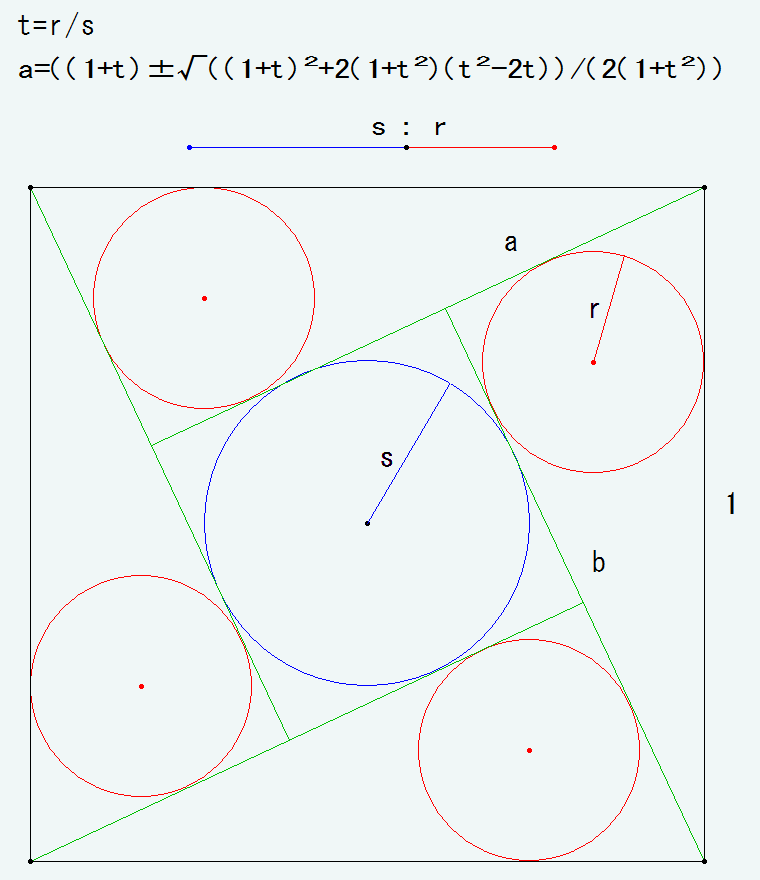
�^����ꂽ�䗦�ŏo����~�̌a��v�Xr�As�Ƃ��Ar/s=t�ƒu���Ɛ}�̎����o���܂��B
����͐����`��1�ӂ�1�Ƃ������̂ŁAa+b-1=2r, b-a(b>a�Ƃ��āj=2s���瓱�������́B
�}���̎��͎l�����Z�ƕ������ł������K�ƃR���p�X�ŋ��߂鎖���o���܂��B
�A���A��̑O���u�}�v�Ƃ��Ă܂����At>1�̎��{�At<1�̎��|�ɂȂ�At=1�̎��́�̒����[���B
���ANo.4300�̓���́A���̎����g���ĕ`�������̂ł��B