今回は定規が主役になりました。

�@緑円の交点を結び、下辺の垂直二等分線と中点Mを作図
�AMと上端の頂点を結び、緑円との交点Pを求める。
�BPと下端の頂点を結び、最初の垂直二等分線との交点Oを求める。
�C図示していませんが、Oを中心に半径OM(OP)の円を描いて完了。

今回も前回と同様、作図工数＝４でした。

作図原理は前回掲載説明（No.4424）を参照下さい。
正方形の一辺の長さを１とし、左下端を原点とすると、点Pの座標は(0.8, 0.6)=(1-0.2, 1-0,4)、言い換えると�Aの直線の傾きが２となり、点Mを通る事が判ります。

No.4424の橙色の直角三角形に着目して下さい。

斜辺が１−ｒ、底辺が１／２、高さがｒですから、ピタゴラスの定理で(1-r)^2=r^2+(1/2)^2
r^2の項が消えますので、1-2r=1/4 ---> 2r=3/4 ---> r=3/8
蛇足：1-r=5/8、1/2=4/8、従って3:4:5の直角三角形♪

半径の計算ができずにコケてます…orz

正方形の一辺の長さを１とすると、簡単な計算で青円の半径は3/8と判ります。
ここから最少作図工数を見付けようとしています。

現在の所、工数＝４
これは明日にでも発表する予定です。

尚、図の橙色の三角形は3:4:5になるのですね。

さすがです。
これ以上の最短手順は無さそうですねぇ。

図で見ると簡単ですねぇ。
しかし、証明はかなり難しそう…

作図手順は４回となりました♪

�@点Pを中心に直線mと交わる適当な赤円を描き、直線との交点の一つをQとする。
�A点Qを中心に半径QPの緑円を描き、図のような交点をRとする。
�B点Rを中心に半径RQの青円を描き、赤円との交点をSとする。
�C点Pと点Sを結んだ直線が求める平行線。

これは菱形を作った描き方で、菱形＝平行四辺形＝描けることの説明終わり。

尚、最初は点Qを求める為に「任意の直線」を使いましたが、最後に結局赤円を描かなければならず５回でした。
出来上がった図を見たら、任意の直線⇒任意の円で１工程減る事に気が付いた次第です。

どうも、最初は正三角形作図に固執していたようです（今回は直線ｍを活用した作図法）。

但し、最少回数である証明は出来ていません。

一応CAD的には描けています（少し古いデータを探し出しました）。
添付図の比率の長方形を作り、対角線を引いて内接円を描いて終わり。

定規とコンパスの場合、直線を引いて、コンパスを有限回使って長さを作ります。
即ち、1.0×10^16：1.5436890140427092×10^16の整数比を作ります。

これをCADで検証すると、キチンと描けています。

検証方法：
�@2本の対角線と長方形の下辺を使って内接円を描く。
�A1本の対角線と正方形の2辺を使って内接円を描く。
�Bこの二つの円をコピーコマンドで円の中心で重ねる。
�C編集コマンドで重複を整理・・・そうすると2円が1円に纏まります。

又�@で作った円と正方形の右辺との交点を求めると、1点のみが表示されます＝CAD的には接している証拠。

しかし、これって描けたと言えるでしょうか？？？

＞やはり計算から出すしかないのですねぇ。
三角形の相似や合同を使って説明出来れば良いのですが．．．
小生にはQ1818の図形的な説明がうまく出てこなかったので、計算に逃げてしまいました。

何故これで描けるかの説明（証明）が無いと、一寸違った図から出発しても描けるのか？
CADの寸法精度の範囲で描けたように見えるのか不安になってしまう＝小生の性格ですね。

添付図の△ADPは直角二等辺三角形です。

また、3つの青円は同径で赤円2つも同径です。

Q1755,Q1761,Q1818の共通した解の図となります。

この図で3題の作図例を考えました。（Q1755は思考停止中・・・）

私の拙い説明より、この図を見ていただいた方が
わかり易いですね。

やはり計算から出すしかないのですねぇ。
最近は計算ができなくなってるからなぁ…orz

＞なぜ描けるのか
これはAB=a、BC=bとし、青円の半径をrとした時、r=(2a+b/2-√(4a^2+b^2/4))/2となっているからです（直角三角形の辺と内接円）。
Q1821で一寸触れていますが、座標計算から導き出し、「小生の解答集２」に動画を掲載済みです。
又、a=3bの時、r=a/2となり作図不可となります＝Q1819はこれに基いた問題でした。

細かい理屈はHIROSHIさんにお願いします。

手数は簡単ですねぇ…
なぜ描けるのかを頑張って考えてみます。

長方形ABCDが与えられ、

�@　中心D、半径DCとなる橙円Dを描き、半径DCが直径CQと
　　なるように延長します。

�A　辺BCの中点MとQを結びます。

�B　三角形CQMの内接円(青円)を描きます。

＊残りの円と接線を描けば完了です。

少し読み違っていました。
�@線を引く（直線との交点を求める）＝１回
�APと上記の交点を使って2円を描く　＝２回
�B２円の交点を結んで中点を求める　＝１回
�C中点から円を描く（直線との交点）＝１回
�Dこの交点と中点を結ぶ（円との交点）＝１回
�E平行線を引く　　　　　　　　　　＝１回

これも７回でした＝７回が最小手数かも．．．

6回がエントリーされました♪

しかし、まだ詳しくフォローしていませんが、「適当な角度」＝45゜でしか使えないような．．．（ＣＡＤの格子点を使った？）

明日にでも再コメントします。

Pを通りmと交差する適当な角度の線を引く。
Pとmの中点を求め、Pとmを直径とする円を描く。
円とｍのもう一方の交点と円の中心を通る線を引く。
この線と円の交点とＰを通過する線がｍと平行。

Q1818とQ1820は全然解けてないです。

手順説明はありませんが、まず最小手数がエントリーしました。

moonlightさん、お久しぶりです。
「正三角形の定理」覗いてみました。定理に自分（？）の名前を付けているのが可愛いですね。

これを見ていると、色々な定理を組み立てていかないと駄目っぽい！
尤も、これ位緻密に積み上げないと出来ないのかも．．．

気力が萎えそうです：理由�@暑さ、�A下の娘がもうすぐ陣痛！
更に言い訳を見付けないと・・・

最小七会！

御無沙汰しております。
1816 の内接する正三角形の話ですが、
正三角形の定理というホームページに
色々面白い事が描いてあります。
ちょっと休みの間の宿題にして色々考えてみます。

気力が続くのが何よりも凄いと思う。
私じゃもうムリだなぁ…

暑い中、頑張っているのですが（No.4402の図参照）：

X0=(a-b/√3)/2=(3a-(√3)b)/6
Y0=(a/√3+b)/2=((√3)a+3b)/6

ここ迄で、(x-X0)^2+(y-Y0)^2=X0^2+Y0^2=(a^2+b^2)/3
結構シンプルな式が出来ましたが、ここから山有り谷有りって感じですね。

脳みそがウニになって来たので、一旦中止するのが正解？？？

もう少し頑張ってみるか！・・・なんか意地になっている感じ！！！

これを考えている途中で、孫に出した易しい問題が浮かんだので、明日にでもアップしよう（＝気分転換）。

かなり難しそうですねぇ…

cosθ=a/s、sinθ=b/sで悪戦苦闘していますが、暑いです！（＝頭が回らない言い訳ですが．．．）
なお、a、b、sは前の図を参照下さい。

「No.4394　Q1816：途中」から今逃げています。
逆にフェルマー点から攻めてみようと思った（前の攻め手を諦めた？）だけ。
猛暑日に図書館で頑張りましたが、道半ばです。
添付の式を整理して、簡素（？）な式が得られれば良いのですが、結果が複雑なら・・・
Q1817からの教訓＝疲れるだけ？？？

解を見ただけで途中計算の膨大さが想像できます。

内接円の半径を計算しました（完）。
添付図一番下の赤枠内のｒが計算結果です。
aは前回同様２の三乗根ですから、当然定木とコンパスでの作図は不可です。

さぁ、Q1816に本格的に挑戦です！！！

＞横：縦(1:1/3)
普通は、横：縦＝３：１と書きますね。

No.4385 Q1817：途中経過の図を参照下さい。
CP1=xの長さが出ましたのでご報告させて頂きます。
a=2^(1/3)・・・三乗根２と置きます。
結果:x=(a^2-2a+4)/5

計算用紙はとても見直せない位『式の羅列』で、検算する元気が全く出てきません。
そこでCADで上記の数値で描いて確認した所、CADの寸法精度内でOKでした。
多分合っているのでしょう。　但し、定木とコンパスでの作図は不可！

次は青円の半径を計算してみます。

横長長方形、横：縦(1:1/3)を超えると無理なようです。

失礼しました。

縦長の長方形は大丈夫みたいですが、横長の長方形では
描けない場合（限界値）が有るようです。

ごめんなさい・・・

今から外出なので、週明けまでには調べておきます。

比率（縦：横）に関係なく、長方形なら描けるようです。

手数の少ない作図法は、青円から描くのが早そうです。

svart enterprise・・・?

三角形に内接する正三角形の作図方法を考えると、次の方法で検討出来ます。
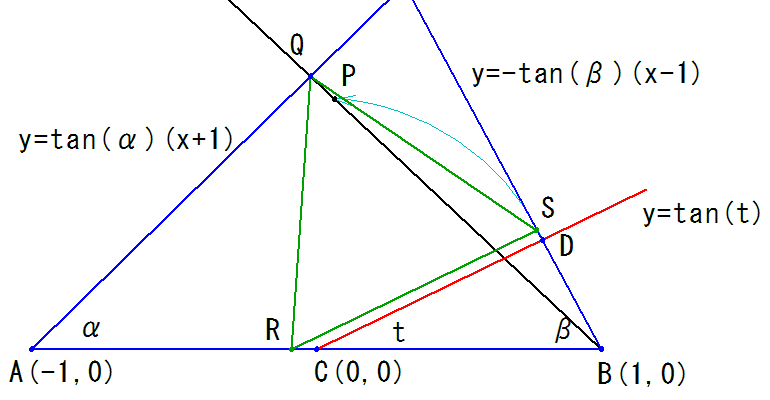
即ち、下辺ABの座標を(-1,0), (1,0)と置き、中点Cから適当な赤線を引いて作図します。
点Cの位置はどこでも良いので、計算し易いようにA、Bの中点としました。
赤線とBから∠βの線との交点をDとします。
Dを60゜回転した点をPとすると、点Pの座標を角度tで表す事が出来ます。
直線BPと点Aから∠αの線との交点をQとすると、内接する正三角形の一辺の長さRSは、CD×BQ/BP。
この長さが最短になれば良いので、tをα、βで示す事が出来ました。

次はフェルマー点の座標をα、βで表す事が出来れば完了です。

しかし、CAD/CAM図形問題からは大分離れて行きますね。
この検証が終わったら、CAD/CAMらしいアプローチを考えてみたいと思います。
Q1817の計算もまだ「最初の一歩」ですので、今世紀中に答えが出るか不安です（と言うより、生きている内に綺麗に解けるか？？？）。

＞赤円が曲者だなぁ。
というよりも、緑円は付け足し（後で簡単に描けるという事）なんですよね。
緑円と青円が接する場合、緑円≡青円となり、長方形はA版（B版）と相似＝1:√2！

＞出張も重なり・・・
まさか「svart enterprise」？？？

これもかなり難しいですねぇ…
赤円が曲者だなぁ。

面積まで考えず、辺の長さが最短である事の説明が付けば良いのですが．．．
正三角形の辺の角度で長さは決まってしまうので（勿論�僊BCの形状によりますが）、三角関数の問題かも・・・

証明は難しそうですねぇ。
式を立てて微分かな？？？

�僊BCで各辺を使って正三角形を作ります（図は�僊CD）。
それらの外接円は一点で交わり、所謂フェルマー点が求まります。
各頂点とフェルマー点を結んだ線に垂直な辺を持つ正三角形。

これが面積最小のようです。

GeoGebraからの推定であり、CADで赤三角形を少し動かすと、面積が確実に増えますが、理論的な説明は？？？

CADで作図してみて下さい。個の三角形の面積を先ず測定します。
次に、頂点のホンの少し隣に点を取り、正三角形を作図して面積を測定します。
どちらに動かしても確実に面積が増えてしまうのですね。しかし理屈が？？？

リュックにパソコンとレポート用紙を入れ、チャリで静かな喫茶店へ！
着いて30分程は厚さが引くのを待っている感じ。
珈琲を飲みながら囲碁問題を解いている内に、やる気がスゥーッと消えていきました。「いつか」頑張ります。
尚、チャリはLSベルハンマーのお蔭で「軽い」ですよ♪（気分的かも知れませんが）

やはり計算ですねぇ。
計算する気力が凄いと思う。

問題図の向きを変えて検討しています。
詳細は図中に記載しました。
この暑さでは続きを計算する気力が・・・

難易度高いですねぇ・・・
今のところ糸口無しの状態です。

独自ではなく、これは線分の二等分から発想を拡げたものです。
緑線が五等分例で、空色線が２〜４等分の作図方法です。

かなり手数が減ってますね。
描き方も独自で凄いです。

点を作図で求める際、定規＋定規、定規＋コンパス、コンパス＋コンパスで交点を求める事になります。
しかし、図形的に意味ある点を求めるには、コンパス+コンパスしかありませんね。

そこで一番少ない工数で交点を求めると、正三角形に辿り着きます。
即ち半径ABを使って２円を描き、二つの交点を得る。
多分最小工数では？

そこから出発したのが添付図です（手順は図中に記載）。
色々検討しましたが、これより短い工数は見付けられていません。
（無い証明は出来ていませんが．．．）

尚、２点A、Bでなく、線分ABが与えられている時、コンパスのみの作図工数は７になります。
定規を使っても殆ど工数が減らないのですね。
この作図方法は「コンパス作図の部屋」を参照下さい（三角形の重心を求める作図の項）。

前の投稿直後に浮かびました。
って、良く見たらN/Tさんのパクリっぽいですね！

こんな別解もあります。
共に、五角形が端の上部に来るのは同じですので、別のを作る予定です。

裏返しＯＫなら別解も多そう。