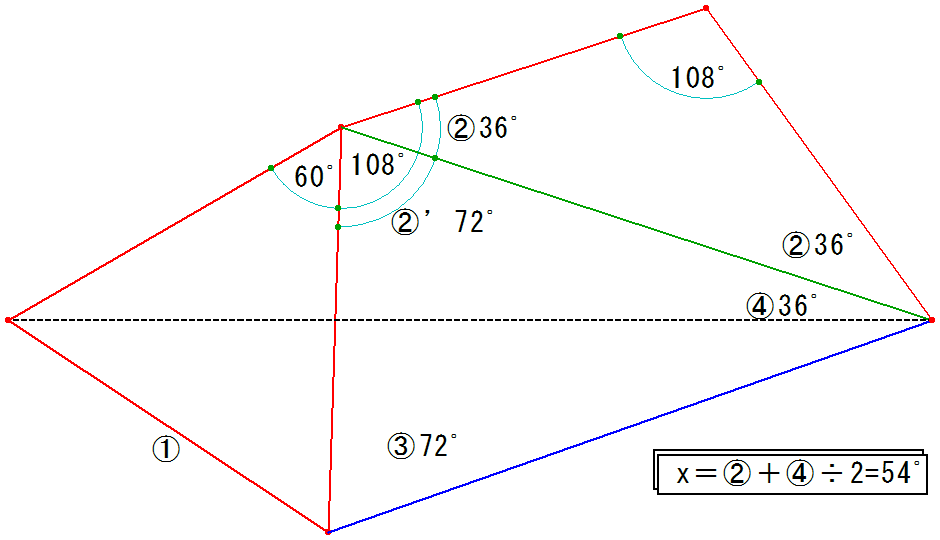
 色々な解き方があるでしょうが、小生は最初に正三角形を作りました(図①)。
色々な解き方があるでしょうが、小生は最初に正三角形を作りました(図①)。
そうすると、168゜は60゜と108゜に分かれます。
②緑線を引いて頂角108゜の二等辺三角形を作ると、底角が36゜で108゜から引いて72゜(②')
③青線を引いて四角形を作ると、赤線の長さが等しく、二つの108゜から等脚台形と判ります⇒底(?)角は72゜。
④赤、緑、青の三角形は底角が等しいので二等辺三角形、従って頂角は36゜
二つの二等辺三角形(正三角形も二等辺三角形の一種)が底辺を共有しているので、夫々の頂角の二等分線(黒破線)は一致。
従って、x=36゜+(36/2)゜=54゜が得られます。
No.4972で紹介した日経の解説は、多分CADで正確な図を描いた為に思い込みしたのかも知れません。
日経の関係者なので理数系が苦手???
上記の(日経のような)ミスを考慮して、添付図では「わざと」不正確な形状を作ってみました。