 FUKUCHAN‚³‚ٌ‚ج•ûگj‚إگ³‰ً‚إ‚·پB
FUKUCHAN‚³‚ٌ‚ج•ûگj‚إگ³‰ً‚إ‚·پB
پu‘S‚ؤ“¯‚¶ژèڈ‡‚إ•`‚¯‚éپv‚ئڈq‚ׂ½‚ج‚حŒê•¾‚ھ‚ ‚è‚ـ‚µ‚½پBژہ‚ح“àپEٹOگع‘ب‰~‚ة‚ح‘®گ«‚ھ‚Qژي—ق‚ ‚é‚ج‚إ‚·پB‚»‚µ‚ؤ‚TٹpŒ`ˆبڈم‚ج“àٹOگع‘ب‰~‚ح”Cˆس‚جگع“_‚ًژو‚ê‚ـ‚¹‚ٌ‚ج‚إپA‘®گ«‚ة‚ ‚ي‚¹‚½ژèڈ‡‚ھ•K—v‚ئ‚ب‚è‚ـ‚·پB
‘®گ«‚PپDگ³‘½ٹpŒ`‚ة“àپEٹOگع‚·‚é‰~‚ً•دٹ·‚µ‚½گ}Œ`
‘½ٹpŒ`‚ج‚à‚ء‚ئ‚à—£‚ꂽ’¸“_“¯ژm‚ًŒ‹‚ش‘خٹpگü‚ح‚P“X‚إŒً‚ي‚è‚ـ‚·پB‚±‚جڈêچ‡پAIJKL‚ئMNOP‚ج“àگع‘ب‰~‚حچ‡“¯‚ئ‚ب‚è‚SٹpŒ`‚جژè–@‚ًژg‚¤‚±‚ئ‚ھ‚إ‚«‚ـ‚·پB“§ژ‹گ}‚ئچl‚¦‚ê‚خ‚à‚ء‚ئ‚à‚ب‚±‚ئ‚إ‚·پBٹïگ”ٹpŒ`‚ة‚آ‚¢‚ؤ‚حŒمڈq‚µ‚ـ‚·پB
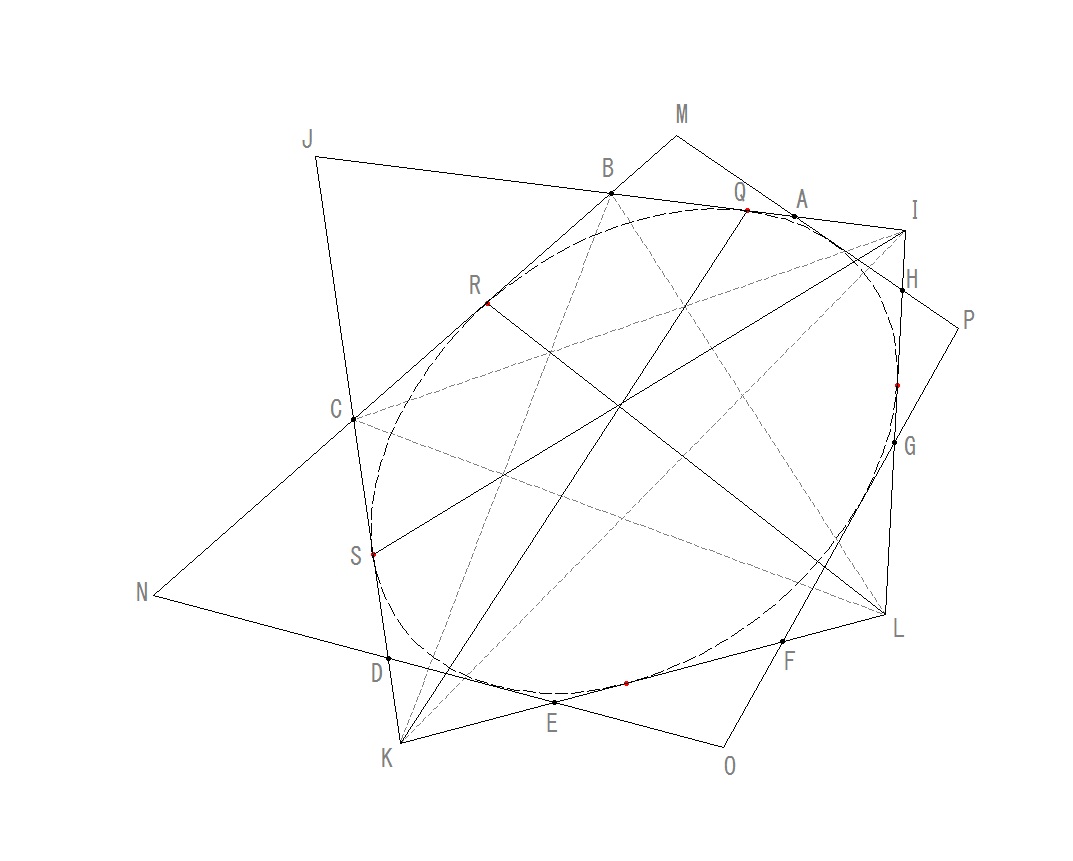
‘®گ«‚QپDˆê”ت“I‚ب“ت‘¼Œ^‘½ٹpŒ`‚ة“àپEٹOگع‚·‚é‘ب‰~‚ً•دٹ·‚µ‚½گ}Œ`
‘خٹpگü‚ح‚P“_‚إŒً‚ي‚è‚ـ‚¹‚ٌپB‚PپD‚ئ“¯‚¶ژè–@‚إ•`‚‚ئIJKL‚ئMNOP‚ج“àگع‘ب‰~‚حچ‡“¯‚ة‚ب‚炸پA‚ا‚؟‚ç‚àABCDEFGH‚ة‚ح“àگع‚إ‚«‚ـ‚¹‚ٌپBˆب‰؛‚جژèڈ‡‚إگع“_‚ً‹پ‚ك‚ـ‚·پB
‚Pپj ‚WٹpŒ`ABCDEFGH‚©‚ç‚TٹpŒ`IBCKL‚ًچى‚éپ@’¸“_‚ج‘g‚فچ‡‚ي‚¹‚ح”Cˆس
‚Qپj ‘خٹpگüIC, BK, CL ‚ًˆّ‚
‚Rپj ’¸“_‚ئ‘خٹpگü‚جŒً“_‚©‚çگع“_Q, R, S ‚ً“¾‚é
‚Sپj ‹ةگüQR, RS‚ج’†“_‚ئ’¸“_B, C ‚©‚ç‘ب‰~‚ج’†گSX ‚ً“¾‚é
ˆب‰؛پA‚SٹpŒ`‚ج“àگع‘ب‰~‚ةڈ€‚·‚é
ٹïگ”‚جگ³‘½ٹpŒ`‚ً•دٹ·‚µ‚½گ}Œ`‚إ‚حپA’¸“_‚ئ‘خ•س‚ة‚à‚ء‚ئ‚à‹ك‚¢‘خٹpگü‚جŒً“_‚ئ‚ًŒ‹‚شگü‚ھ‚P“_‚إŒً‚ي‚è‚ـ‚·پB“Y•t‚جŒـٹpŒ`IBCKL‚إ‚حIS, KQ, LR‚ة‘ٹ“–‚µ‚ـ‚·پBŒ©گh‚¢‚إ‚·‚ھ‚±‚جگ}‚إ‚ح‚Rگü‚ھˆê“_‚إŒً‚ي‚ء‚ؤ‚¢‚ـ‚¹‚ٌپBڈ]‚¢‚±‚جگ}Œ`‚حگ³‚TٹpŒ`‚ج•دٹ·گ}‚إ‚ح‚ ‚è‚ـ‚¹‚ٌپB‚QپD‚جژèڈ‡‚ًژg‚¤‚±‚ئ‚ة‚ب‚è‚ـ‚·پB