 ‚â‚ح‚èپA”½‰‚ھˆ«‚‚ب‚è‚ـ‚µ‚½پB
‚â‚ح‚èپA”½‰‚ھˆ«‚‚ب‚è‚ـ‚µ‚½پB
‚±‚ج–â‘è‚حژً“]“¶ژq‚³‚ٌ‚ج•”‰®‚©‚ç
پمپi•½•ûچھپj‚جچىگ}‚إ‹پ‚ك‚ç‚ê‚ـ‚·پB
چىگ}—ل‚ح1/3‚ج–تگد‚جچىگ}‚إ‚·پB
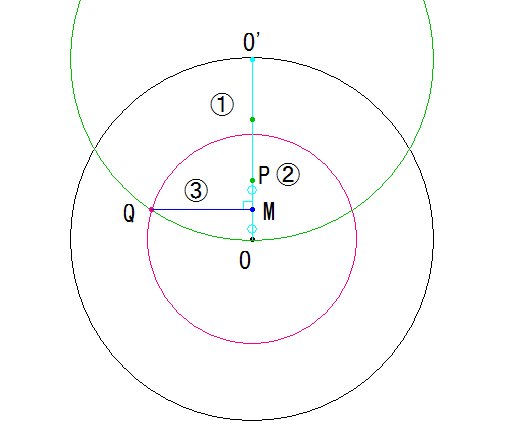
‡@”¼ŒaO O'‚ًˆّ‚«پA‰~O‚ئ“¯Œa‚ج—خ‰~O'‚ً“_O'‚ً’†گS‚ة•`‚«‚ـ‚·پB
‡A”¼ŒaO O'‚ً3•ھٹ„‚ة•ھ‚¯پA’†گSO‚ج‘¤‹ك‚ًP‚ئ‚µ‚ـ‚·پB
‡Bگü•ھPO‚جگ‚’¼“ٌ“™•ھگü‚ئ—خ‰~O'‚جŒً“_‚ًQ‚ئ‚µ‚ـ‚·پB
پ–”¼ŒaOQ‚ھ‹پ‚ك‚é‰~‚إ‚·پB
‚ب‚¨پA•ھٹ„(2,3,4پEپEپE‚ژ):–تگد(1/2,1/3,1/4پEپEپE1/n)
‚ئ‚ب‚è‚ـ‚·پB
پE”{گد‚à“¯‚¶چىگ}–@‚إ‚·‚ھپAڈپX‚جŒvژZ‚ئ”P‚è‚ھ•K—v‚إ‚·پB
ژً“]“¶ژq‚³‚ٌ‚ضٹ´ژس‚ج–â‘è‚إ‚µ‚½پB‚إ‚حپA‚±‚ê‚ة‚ؤپEپEپE